CSCI 3321 Assignment #5
Numerical Solution of a Two-Point Boundary-Value Problem
(Caution: Do NOT wait until the last minute!)
Construct a computer program that uses both the secant method and the Runge-Kutta method (that you developed in assignment #4) to obtain a numerical solution to the two-point boundary-value problem:
x' = f(t,x) = x + 0.09 x 2 + cos(10 t) differential equation
x(0) + x(1) - 3.0 =
0
boundary condition
Starting with the initial
guesses 0.7 and 1.0 for the (unknown) initial
value, x(0), obtain an approximation to x(0) {for the final
solution, x(t)} such that the boundary condition is satisfied
to within a tolerance of 10-4 . Use a fixed
stepsize of 0.025 (i.e., take 40 steps each time you integrate
the differential equation from t=0 to t=1). Write your
program so that the output shows the values of x(0), x(1), and
x(0)+x(1)-3 (the error in satisfying the boundary condition)
at the end of each iteration of the secant method. After the
last iteration of the secant method, re-integrate from t=0 to
t=1 and print out the solution for x(t) over the range
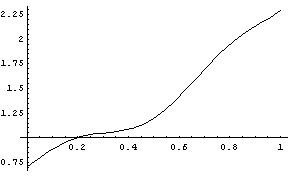
[0,1]. Your solution for x(t) should resemble the
solution plotted below.
Also, your approximation to x(0), when you finish, should be
roughly 0.7378743818.

.