|
T. Andrew Yang
|
last updated: 3/21/2011 |
||||||||||||||||||||||||||||||||||||||||
|
Total points= 50 (oral
presentation) + 50 (written report) Find a topic of your interests related to ethical
issues in computer usage, development, and operations. -
Requirements: a)
Three deliverables are required of each student. See the syllabus for
the respective due dates. §
A draft of your paper – to be posted to the class discussion
board. §
An oral presentation (of 5~10 minutes) of your topic – to be
presented to the whole class. §
A two-page paper on the topic – to be emailed to yang@uhcl.edu. b)
Your paper should cite three or more technical articles. Do not use
only web links; at least two of the cited articles must be refereed journal
or conference papers. c)
Proper citing should be practiced when writing the paper. Visit http://sce.uhcl.edu/yang/citing.htm
to learn how to do proper citing in a research paper. Visit http://sce.uhcl.edu/yang/research/index.htm
for sample research articles. -
Grading
criteria: 1)
40% Relevance: The chosen topic must be relevant to computer ethics. 2)
30% Technical strength: The paper should be written to demonstrate your
knowledge in the chosen topic and your technical writing ability. Coherency
is especially important. 3)
30% Cited references: See b and c above. Go to the Index Total points= 110 1.1.
(10 pts)
Visit the class discussion group at http://groups.google.com/group/csci3333spring2011?hl=en. Post a message with your full name as the subject
line. In your post, briefly introduce yourself (including your full name) and
one item you most desire to learn in this class. Throughout this class, you
shall regularly participate at the discussion group to find recent
announcements, reminders, and discussions.
1.2. Algorithm Analysis
Read Chapter 5 of
the textbook. Understand Figure 5.3, which shows the various functions in
order of increasing growth rates. The following
questions are based on a one-dimensional array A of 100,000 integers. 1.2.1.As
stated in Sec 5.6.1 in the text, the sequential
search algorithm steps through the array sequentially until a match is
found or when all the items in the array have been examined. In the latter
case, the algorithm returns ‘not found’ as the search result.
Suppose you use sequential search
to determine the location of a given item n in the array (or to report that n
does not exist in the array).
1.2.1.1. (5 pts) What is the fewest number of
array items in A that need to be
examined in order to solve the problem (i.e., the best scenario)?
1.2.1.2. (5 pts) What is the largest number of
array items that need to be examined in order to solve the problem (the worst
scenario)?
1.2.1.3. (5 pts) What is the average number of
array items that need to be examined in order to solve the problem (the
average scenario)?
1.2.1.4. (5 pts) Explain what it means by saying
that the growth rate of the sequential search algorithm is O(N). N represents
the number of items in the array.
1.2.2.
Sample programs from the book are
available on line at http://users.cis.fiu.edu/~weiss/dsj4/code/.
The following set of exercises are based on the program MaxSumTest.java, which is one of the sample applications for
Chapter 5. Visit http://users.cis.fiu.edu/~weiss/dsj4/code/MaxSumTest.java
to download it directly.
1.2.2.1. (5 pts) Run MaxSumTest.java and capture the screen snapshot showing the
complete execution of that application. Attach the captured snapshot.
1.2.2.2. (5 pts) Explain why algorithm #1 is not
run when N = 100000 and N = 1000000.
1.2.2.3. (5 pts) Complete Table 1 (below) by
fill in the values generated by running the program.
Table 1. The efficiency of various algorithms given
different sizes of arrays
1.2.2.4. (5 pts) Compare the values between the first
two rows (algorithms #4 and #3). Explain why algorithm #4 consistently takes
more time than algorithm #3, given different values of N.
1.2.2.5. (5 pts) Compare the values between the
algorithms #4 and #2, and explain why algorithm #4 consistently takes less time
than algorithm #2, given different values of N.
1.2.2.6. (5 pts) Explain why algorithm #1 is the
slowest among the four.
1.2.3. Modify
the main( ) method in MaxSumTest.java such that the screen output
generated by the revised program resembles Table 1 above. Hints: You may use
a two-dimensional array to store the results, and then have the values in the
array displayed. Alternatively four separate one-dimensional arrays may be
used.
Note about documentation: Proper
documentation should be practiced when writing/revising your source programs.
Give appropriate information as comments and use proper indentations.
Always have your name appear at the beginning of the program as the
author or reviser of the program.
1.2.3.1. (30 pts) Attach the revised program and
the captured screen output.
1.2.3.2. (20 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
Go to the Index Total points= 130 2.1. Programming Projects
Note: For the ‘Programming Projects’ part,
students may choose to use C, C++, or Java as the implementation language.
2.1.1. Project
description: As stated in Exercise 5.40 in the textbook (page
225), the Sieve of Eratosthenes is a method used to compute all primes less
than a given integer N. Begin by making a table of integers 2 to N. Find the
smallest integer, i, that is not crossed out yet in the table. Then print i
and cross out i, 2i, 3i, etc., from the table. When i > squareRoot (N),
i.e., i2 > N, the algorithm terminates.
Further discussions about the method can be found at http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes.
A Java implementation of the algorithm can be found at http://www.cs.princeton.edu/introcs/14array/PrimeSieve.java.html
and is copied below.
2.1.2. Project
requirements:
In this project, you are required to do the
following:
a.
Write a function or method to implement the
Sieve of Eratosthenes method of calculating number of primes less than a
given integer N. Let’s call the method primeSieve (int N).
b.
Set up a main program similar to MaxSumTest in Lab 1.2.2 to measure the
respective elapsed time when running
|
|||||||||||||||||||||||||||||||||||||||||
|
/** class: Employee Three arrays are used to represent the employee
information. **/ public class Employee { //
attributes private
final int capacity=10; private
int [ ] ID = new int [capacity]; private
String [ ] name = new String [capacity]; private
double [ ] salary = new double [capacity]; int
current=0; //next position to add data //
methods //
add( ): add a new employee public
void add (int id, String empName, double empSalary ) { System.out.println
("add()"); if
(current < capacity) { ID[current]
= id; name[current]
= empName; salary[current]
= empSalary; current++; }
//if }
// add( ) //
remove( ): remove an employee public
void removeByID (int ID ) { System.out.println
("removeByID()"); }
// remove( ) //
averageSalary( ): return the average of all employees' salaries public
double averageSalary( ) { System.out.println
("averageSalary()"); }
//averageSalary( ) //
displayAll ( ): display all employees' information public
void displayAll ( ) { System.out.println
("displayAll()"); System.out.println
("\tID\tName\t\t\tSalary"); System.out.println
("\t-----\t--------------------\t---------"); for
(int i=0; i < current; i++) { System.out.println
("\t" + ID[i] + "\t" + name[i] + "\t\t" +
salary[i]); } }
//displayAll ( ) } //Employee class |
Table 3. Source program EmployeeArraysTest.java
|
/** EmployeeArraysTest.java Using multiple arrays to store employee records. **/ public class EmployeeArraysTest { //
main( ) ------------------- public
static void main (String args[]) { Employee
empList = new Employee(); empList.add(11111,
"John Doe", 55000); empList.add(22222,
"Jane Doe", 66000); empList.add(33333,
"Bill Smith", 44000); empList.add(44444,
"Adam King", 188000); empList.add(55555,
"Josh London", 120000); empList.displayAll(); }
// main } // EmployeeArraysTest class |
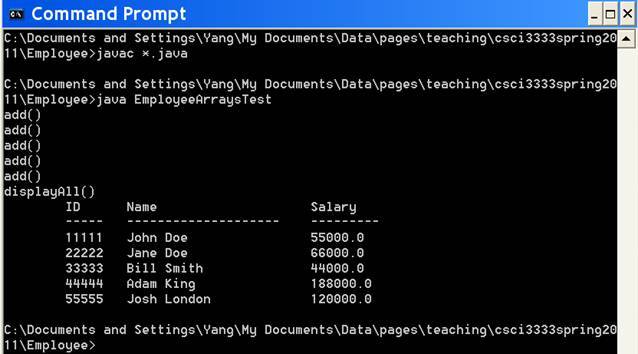
Figure 1. Running EmployeeArraysTest.java
3.1.1.
(continued
from 3.1.1) Complete the removeByID( ) method.
When it is called, given an employee’s ID, that employee’s
information will be removed from the arrays.
Note1: When the employee is not in the arrays, display an
appropriate message.
Note2: When the removed employee is not the last employee in the
arrays, the rest of the employees need to be moved up to fill the emptied
space.
Use the revised main( ) method as shown in Table 4 to test
the removeByID( ) method.
Table 4. Revised testing program
|
public class EmployeeArraysTest { //
main( ) ------------------- public
static void main (String args[]) { Employee
empList = new Employee(); empList.add(11111,
"John Doe", 55000); empList.add(22222,
"Jane Doe", 66000); empList.add(33333,
"Bill Smith", 44000); empList.add(44444,
"Adam King", 188000); empList.add(55555,
"Josh London", 120000); empList.displayAll(); empList.removeByID(33333); empList.add(66666,
"Jack London", 220000); empList.removeByID(22555); empList.displayAll(); }
// main } // EmployeeArraysTest class |
3.1.1.1.
(15 pts)
Attach
the revised programs and screen output.
3.1.1.2.
(10 pts) Give the TA a demo of
your revised application.
3.1.2.
(continued
from 3.1.1) Revise the add( ) method such
that the employee records will be saved in the arrays at ascending order,
according to the employee ID.
Use the
revised main( ) method as shown in Table 5 to test your revised Employee class.
Table 5. Revised testing program (2)
|
public class EmployeeArraysTest { //
main( ) ------------------- public
static void main (String args[]) { Employee
empList = new Employee(); empList.add(33333,
"Bill Smith", 44000); empList.add(55555,
"Josh London", 120000); empList.add(22222,
"Jane Doe", 66000); empList.add(44444,
"Adam King", 188000); empList.add(11111,
"John Doe", 55000); empList.add(33355,
"Meredith London", 111000); empList.add(22666,
"Jack London", 220000); empList.add(34566,
"M. Paris", 255000); empList.displayAll(); }
// main } // EmployeeArraysTest class |
3.1.2.1.
(15 pts)
Attach
the revised programs and screen output.
3.1.2.2.
(10 pts) Give the TA a demo of
your revised application.
3.1.3.
(continued
from 3.1.1) Complete the averageSalary( )
method, such that it will return the average salary of all employees.
Revise the
method displayAll( ) such that it
will first display the employee information, and then display the average
salary of all employees. See Figure 2 for a sample output.
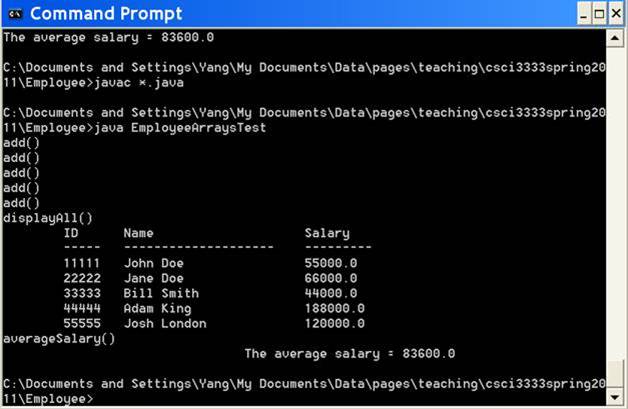
Figure 2. Sample output of running EmployeeArraysTest.java (2)
3.1.3.1.
(15 pts)
Attach
the revised programs and screen output.
3.1.3.2.
(10 pts) Give the TA a demo of
your revised application.
3.2.
A class called java.util.ArrayList
is provided in
Java. ArrayList is a resizable-array
implementation of the List interface. Methods such as size(), isEmpty(),
get(),
set(),
remove(),
and contains()are
provided in ArrayList. See http://download.oracle.com/javase/6/docs/api/java/util/ArrayList.html
for the attributes and methods defined for that class in JSE 6.0.
Visit http://leepoint.net/notes-java/data/collections/lists/arraylist.html
to learn the trade-offs between regular arrays and ArrayLists.
Requirements:
In Table 2,
the class Employee is defined as an object of three arrays. A typical
object-oriented approach is to define the Employee class in such a way that
each instance of Employee consists of three attributes ID, name, and salary.
Let’s name the new class EmployeeOO.
(1)
First, define the EmployeeOO class. Follow object-oriented programming
conventions to define the various get( ) and set( ) methods for this class.
(2)
Write a testing program to test the EmployeeOO class. In the main()
method, declare an ArrayList of EmployeeOO.
(3)
Also in the main( ) method, use the Collections.sort(
) method to sort the ArrayList. Show the content of the list before
and after the sorting.
Hint: View http://onjava.com/pub/a/onjava/2003/03/12/java_comp.html?page=1
for information about implementing Comparable.
http://www.wellho.net/mouth/1502_Java-sorting-ArrayList-example-generics.html
provides example programs for implementing more than one comparator.
3.2.1.
(70 pts)
Attach
the source programs and screen output.
3.2.2.
(30 pts) Give the TA a demo of
your revised application.
Go to the Index
Total points= 100 + 35 (bonus
points)
4.1.
(15 pts)
Exercise 5.16
4.2.
(20 pts) Exercise
5.34. Devise an algorithm of O(N)
to solve the problem.
4.3.
(15 pts, 3 pts each) Exercises 7.17b,
7.18a, 7.18b, 7.19a, 7.19b
4.4.
(15 pts) A
sequence and two explicit formulas are given in Figure 4.1. Use Theorem 7.2
from the book to complete the proof by induction.

Figure 4.1 Two
formulas for a recurrent sequence
4.5.
This
exercise is based on the ListNode.java
program, available from http://sce.uhcl.edu/yang/teaching/ListNode.htm.
4.5.1.
Complete
the addSorted (int value) method,
which takes an integer and adds it into the linked list while maintaining
ascending order of the items in the list. Use the main( ) method as shown in
Figure 4.2 to test the addSorted( ) method. Sample output of running the
program is also shown in Figure 4.2.
Note: The return type of the addSorted( ) method has been
changed to ListNode2.
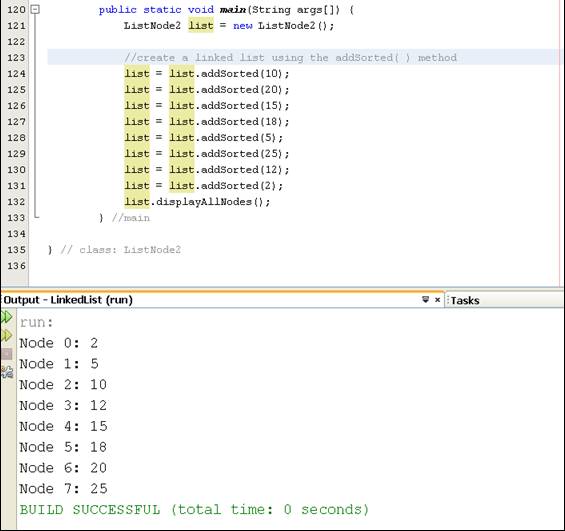
Figure 4.2 The
main( ) method for testing addSorted( ), along with sample screen output
4.5.1.1.
(20 pts) Attach the revised source
program and screen output.
4.5.1.2.
(15 pts) Give the TA a demo of your revised application.
4.5.2.
(Bonus project) (Optional) A linked list is a recursively defined data
structure. Each node itself is the beginning of a linked list. Write a
recursive method addSortedRecursive ( ). Instead of using a loop to determine
where to add the new node, this method adds the new value into the list by
recursively calling itself. Below is a sketch of the method.
public ListNode addSortedRecursive (ListNode list,
int value ) {
if the current node’s
value is > value
create a new node and add value into it;
add the new node in front of the current node;
return the new node;
else
return addSortedRecursive (
list.next, value ); //add the value to the linked list after the current
node
}
4.5.2.1.
(20 pts) Attach the revised source program and screen output.
4.5.2.2.
(15 pts) Give the TA a demo of your revised application.
Go to the Index
Total points=100 + 60 (bonus
points)
5.1. (15 pts) Exercise 18.1.
5.2. (15 pts) Exercise 18.3.
5.3. (15 pts) Exercise 18.4.
(Note: Only the inorder traversal
is needed.)
5.4. (15 pts) Exercise 18.6.
5.5. (15 pts) Exercise 19.1.
5.6. (25 pts) Exercise 20.5.
5.7. (Bonus exercises, optional)
5.7.1. (30 pts) Exercise 19.2.
5.7.2. (30 pts) Exercise 20.11.
Go to the Index