CSCI 5333 Data Base Management
System
Spring 2002 (1/14-5/6)
Chapter 14: Functional Dependencies & Normalization
- Objective: To provide some formal
measure of why one grouping of attributes into a relation schema may
be better than another.
- Two levels at which we can discuss the "goodness"
of relation schemas:
- The logical (or conceptual) level—how users
interpret the relation schemas and the meaning of their attributes.
- The implementation (or storage) level—how the
tuples in a base relation are stored and updated.
- NOTE: The relational database design theory developed
in this chapter applies mainly to base relations.
- design by synthesis (bottom-up; attributes to
relations) versus design by analysis (top-down; relations to decomposition)
- Functional dependency: A formal constraint among
attributes that is the main tool for formally measuring the appropriateness
of attribute groupings into relation schemas.
- Normalization: A process of analyzing relations
to meet increasingly more stringent requirements leading to progressively
better groupings, or higher normal forms.
Ø
Go to the Index
14.1 Informal Design Guidelines for
Relation Schemas
- The semantics of
a relation: (informal definition) What the collection of attributes
mean in a relation; Or how the attributes of a relation can be interpreted.
- Simple cases: EMPLOYEE, DEPT
- More complex cases: What is the semantics of the
WORKS_ON relation? How about the DEPT_LOCATIONS relation?
- GUIDELINE 1: Design a relation
schema so that it is easy to explain its meaning. Do not combine attributes
from multiple entity types and relationship types into a single relation.
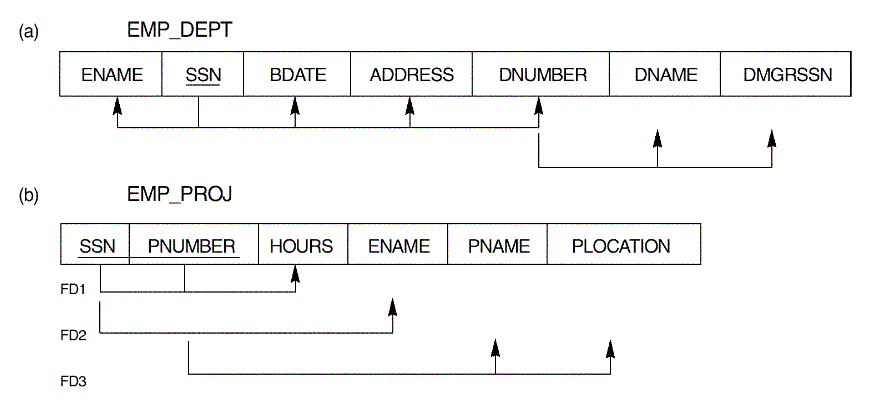
- Examples of relations with mixed attributes: Fig.
14.3
- Question: What kind of problem may be caused by
the above schema?
- Problem 1: Redundant storage of data
- Problem 2: Update anomalies
- Exercise: Explain what 'insertion anomaly'
is by using the relation EMP_DEPT in Fig. 14.4.
- Question: Why 'insertion anomaly' is
not a problem with the relational database schema in Fig. 14.2?
- Exercise: Define what 'insertion anomaly'
is.
- Exercise: Define what 'deletion anomaly'
is.
- Exercise: Define what 'modification
anomaly' is.
- GUIDELINE 2: Design the
base relation schemas so that no insertion, deletion, or modification
anomalies are present in the relations.
- Consideration between "good design" versus "performance".
- GUIDELINE 3: As far as
possible, avoid placing attributes in a base relation whose values may
frequently be null. If nulls are unavoidable, make sure that they apply
in exceptional cases only and do not apply to a majority of tuples in the
relation.
- Question: Explain what 'spurious tuples' are.
- GUIDELINE 4: Design
relation schemas so that they can be JOINed with equality conditions
on attributes that are either primary keys or foreign keys in a way that
guarantees that no spurious tuples are generated.
See also the nonadditive (or lossless) join property
in Ch. 15.
Ø
Go to the Index
14.2 Functional Dependencies
- The concept of describing the whole database
as a single universal relation schema.
- Informal definition: A functional dependency
is a constraint between two sets of attributes from the database.
- Formal definition:
- A functional dependency, denoted by X
--> Y, between two sets of attributes X and Y that are subsets of R
specifies a constraint on the possible tuples that can form a relation
state r of R. The constraint is that, for any two tuples t1 and t2 in r
that have t 1[X] = t2[X], we must also have t
1[Y] = t2[Y].
- That is, the values of the Y component
of a tuple in r depend on the values of the X component.
- Or, there is a functional dependency
from X to Y.
- The set of attributes X is called the
left-hand side of the FD, and Y is called the right-hand
side .
- X functionally determines Y in a relation
schema R if and only if, whenever two tuples of r(R) agree on their X-value,
they must necessarily agree on their Y-value.
- If X is a candidate key of R, then there
exists a FD from X to Y for any subset of attributes Y of R.
- The main use of functional dependencies
is to describe further a relation schema R by specifying constraints on
its attributes that must hold at all times.
- Relation extensions r(R) that satisfy
the functional dependency constraints are called legal extensions
(or legal relation states) of R.
- Examples: (See Fig. 14-3b above.)
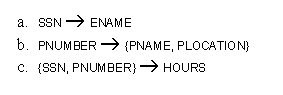
- A functional dependency is a property
of the relation schema (intension) R, not of a particular legal
relation state (extension) r of R. That is, a functional
dependency must hold for ALL the extensions of R.
- Inference Rules for Functional Dependencies
- F is the set
of functional dependencies that are specified on relation schema R.
- F+
is the set of all possible functional dependencies that may
hold on R, and is called the closure of
F .
- That is, F+
is the set of all functional dependencies that can be inferred
from F.
- An FD f
is inferred from a set of dependencies F specified on R if
f holds in every relation state r that is a legal extension
of R .

- Inference rules IR1 through IR3
are known as Armstrong’s inference rules.
- Inference rules IR1 through IR3
are sound and complete
.
- By sound, we mean that,
given a set of functional dependencies F specified on a relation schema
R, any dependency that we can infer from F by using IR1 through IR3 holds
in every relation state r of R that satisfies the dependencies in F.
- By complete, we mean that
using IR1 through IR3 repeatedly to infer dependencies until no more dependencies
can be inferred results in the complete set of all possible dependencies
that can be inferred from F, that is, the closure of F.
- Determine the closure of
X under F: For each set of attributes X, we determine the set
of attributes that are functionally determined by X based on F.

- Exercise: Apply
algorithm 14.1 to the following set of FDs.
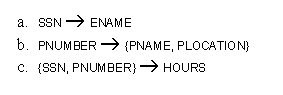
- Exercise 14-20:
Consider the relation schema EMP_DEPT in Figure 14.3(a)
and the following set G of functional dependencies on EMP_DEPT: G = {SSN
-> {ENAME, BDATE, ADDRESS, DNUMBER}, DNUMBER -> {DNAME,
DMGRSSN}}. Calculate the closures {SSN}+ and {DNUMBER}
+ with respect to G.
- A set of functional dependencies
E is covered by a set of functional dependencies F if every FD
in E is also in F+.
- Two sets of functional dependencies
E and F are equivalent if E
+ = F+.
- If two sets of
functional dependencies E and F are equivalent,
then E covers F and F covers E.
- Note: Algorithm 14.2 (finding
a minimal cover of a given set of functional dependencies) will be discussed
at the beginning of chapter 15.
- The equivalency between two sets of functional dependencies
- Given
two sets of functional dependencies, F and G, how would you prove that
F and G are equivalent?
Answer: Prove that
F covers G AND G
covers F. Both must be true.
- How would you
prove that F covers G? See page 482: 14.2.3.
- Approach 1: Show that each fd in G is also in F+.
For each FD X --> Y in G:
Show
that FD can be inferred by the functional dependencies in F.
If you can
show that for each FD in G, then G is covered by F.
- Approach 2: Calculate X+ under F for each fd (X
--> Y) in G.
For each FD X --> Y in G:
a. Calculate X+ under F.
b. Determine if X+
under F contains Y.
If the answer to step
b above is true for each FD in G, then G is covered by F.
NOTE:
X+ must be calculated under F, not under G.
Ø
Go to the Index
|