CSCI 5333 Data Base Management
System
Spring 2002 (1/14-5/6)
Chapter 14 (Part B)
: Normalization
- Normal Forms: 1NF, 2NF, 3NF, BCNF, 4NF, 5NF
14.3 + 14.4 Normal Forms Based on Primary Keys
- 1NF, 2NF, 3NF: proposed
by Codd in 1972.
- Normalization of data: A process
of analyzing the given relation schemas based on their FDs and primary
keys to achieve the desirable properties of (1) minimizing redundancy and
(2) minimizing the insertion, deletion, and update anomalies discussed in
Section 14.1.2.
- Normalization through decomposition:
Unsatisfactory relation schemas that do not meet certain conditions—the
normal form tests—are decomposed into smaller relation schemas that meet
the tests.
- Two critical properties with respect to the process
of normalization through decomposition:
- The lossless join (or nonadditive join) property
- The dependency preservation property
- Review of 'keys':
- If a relation schema has more than one key, each
is called a candidate key.
- One of the candidate keys is arbitrarily designated
to be the primary key, and the others are called secondary keys
.
- Each relation schema must have a primary key.
- A prime attribute of
relation schema R: An attribute which is a member of some candidate
key of R.
- First normal form (1NF):
- The value of any attribute in a tuple
must be an atomic value.
- Part of the formal definition of a relation in
the basic (flat) relational model.
- An example of a relation which is not 1NF: See
Fig. 14.8 (a).
- Fig. 14.9: How to normalize a nested relation
.
- A simpified definition: A relation schema
R is in 2NF if every nonprime
attribute A in R is fully functionally dependent
on the primary key of R. (NOTE: This definition
is replaced by the general definition.)
- A functional dependency X --> Y is a full
functional dependency if removal of any attribute A from X means that
the dependency does not hold any more.
- A relation that is in 1NF but not in 2NF: Fig.
14.3 (b).
- Fig. 14.10(a): Convert the relation in 14.3(b)
to relations in 2NF.
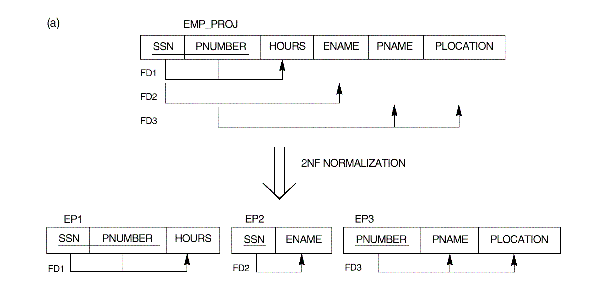
- A general definition
of 2NF (p.491): A relation schema R is in 2NF if every nonprime attribute
A in R is not partially dependent on any key of R.
- A relation schema R is in 3NF if it satisfies
2NF and no nonprime attribute of R is transitively dependent
on the primary key.
- A functional dependency X --> Y in a
relation schema R is a transitive dependency if there is a set of
attributes Z that is neither a candidate key nor a subset of any key of
R, and both X --> Z and Z -->Y hold.
- Example: The relation schema EMP_DEPT in
Figure 14.3(a) is in 2NF but not in 3NF, because of the transitive dependency
of DMGRSSN (and also DNAME) on SSN via DNUMBER.
- Fig. 14.3 (b): Convert a relation in 2NF
to 3NF.

- Alternative definition of 3NF (from 14.4):
A relation schema R is in third normal
form (3NF) if, whenever a nontrivial functional dependency X
--> A holds in R, either (a) X is a superkey of R, or (b) A is a prime
attribute of R.
To prove that R is NOT in 3NF: Try to find
a nontrivial functional dependency in which the
left hand side is NOT a superkey AND the right hand side is NOT a prime attribute.
-
A general alternative definition of 3NF:
A relation schema R is in 3NF if every
nonprime attribute of R meets both of the
following terms:
- It is fully functionally dependent
on every key of R.
- It is nontransitively dependent
on every key of R.
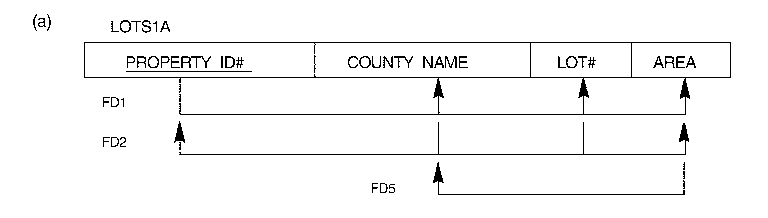
NOTE: In an attempt to
apply this criteria to the relation schema LOTS1A (on page 492), the relation
schema does not seem to pass this test. However, if the general definition
of 'transitive dependency' (as defined on page 489; Also see footnote #13
on the same page) is adopted, LOTS1A is actually in 3NF.
- Table 14.1 (p.490): Summary
of Normal Forms Based on Primary Keys and Corresponding Normalization.
Ø
Go to the
Index
14.5 Boyce-Codd Normal Form
- A relation schema R is in
BCNF if whenever a nontrivial
functional dependency X --> A holds in R, then X is a superkey
of R.
- A relation which is in 3NF but
not in BCNF: Fig. 14.12 (a):
- Converting a 3NF into relations
in BCNF: Fig. 14.12 (b)

- Exercise 14.24:
Prove that any relation schema with two attributes is in BCNF.
Ø
Go to the
Index
|



