|
T. Andrew Yang
|
last updated: 10/21/2011 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Total points= 50 (oral
presentation) + 50 (written report) Find a topic of your interests related to ethical
issues in computer usage, development, and operations. -
Requirements: a)
Three deliverables are required of each student. See the syllabus for
the respective due dates. §
A draft of your paper – to be posted to the class discussion
board. §
An oral presentation (about 5 minutes) of your topic – to be
presented to the whole class. §
A two-page paper on the topic – to be emailed to the instructor (yang@uhcl.edu). b)
Your paper should cite three or more technical articles. Do not
use only web links; at least two of the cited articles must be
refereed journal or conference papers. c)
Proper citing should be practiced when writing the paper. Visit http://sce.uhcl.edu/yang/citing.htm
to learn how to do proper citing in a research paper. Visit http://sce.uhcl.edu/yang/research/index.htm
for sample research articles. -
Grading
criteria: 1)
40% Relevance: The chosen topic must be relevant to computer ethics. 2)
30% Technical strength: The paper should be written to demonstrate your
knowledge in the chosen topic and your technical writing ability. Coherency
is especially important. 3)
30% Cited references: See b and c above. Go to the Index Total points= 100 1.
(5 pts) Visit the class discussion board in
the UHCL BlackBoard (https://blackboard9.uhcl.edu/webapps/login/). Post
a message with your full name as the subject line. In your post, briefly
introduce yourself (including your full name) and one item you most desire to
learn in this class. Throughout this class, you shall regularly participate
at the discussion group to find recent announcements, reminders, and
discussions.
2. Algorithm Analysis
Read Chapter 5 of
the textbook. Study and understand Figure
5.3, which shows various functions in order of increasing growth rates. Assumptions: The following questions are based on a
one-dimensional array A of 275,000 integers. 2.1.1.As
stated in Sec 5.6.1 in the text, the sequential
search algorithm steps through the array sequentially until a match is
found or when all the items in the array have been examined. In the
latter case, the algorithm returns ‘not found’ as the search
result. Suppose you use sequential
search to determine the location of a given item n in the array (or to
report that n does not exist in the array).
2.1.1.1. (5 pts) What is
the fewest number of array items in A
that need to be examined in order to solve the problem (i.e., the best
scenario)? Justify your answer.
(That is, explain how your answer is correct.)
2.1.1.2. (5 pts) What is
the largest number of array items that need to be examined in order to solve
the problem (the worst scenario)?
Justify your answer.
2.1.1.3. (5 pts) What is
the average number of array items that need to be examined in order to solve
the problem (the average scenario)?
Justify your answer.
2.1.1.4. (10 pts) Explain
what it means by saying that the growth rate of the sequential search
algorithm is O(N). N represents the number of items
in the array.
2.1.2.
Sample programs from the book are
available on line at http://users.cis.fiu.edu/~weiss/dsj4/code/.
The following set of exercises are based on the
program MaxSumTest.java, which is
one of the sample applications for Chapter 5. Visit http://users.cis.fiu.edu/~weiss/dsj4/code/MaxSumTest.java
to download it directly (local
copy).
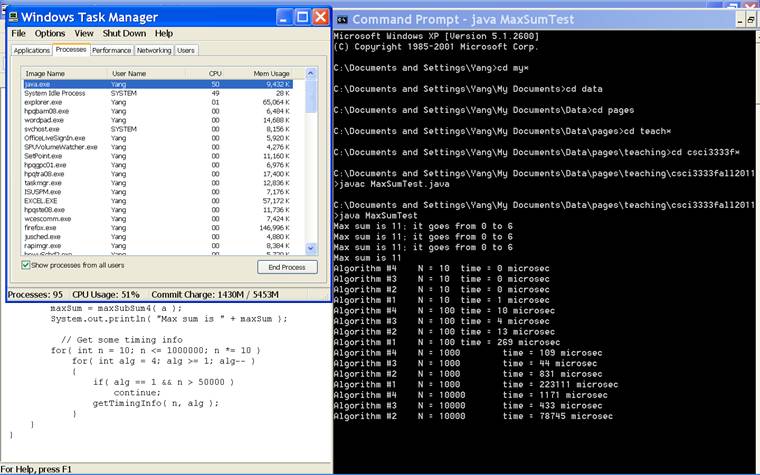
2.1.2.1. (10 pts) Run MaxSumTest.java and capture the screen snapshot
showing the complete execution of that application. Attach the
captured snapshot.
Note: The captured screen snapshot should show that the java program is
using a high percentage of the computer’s CPU. You may use Windows Task
Manager to see that. A sample snapshot showing partial execution of
the program and the cpu usage by that program is
shown below.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Size of N
Algorithms
|
250
|
2500
|
25000
|
250000
|
2500000
|
#4
|
|
|
|
|
|
#3
|
|
|
|
|
|
#2
|
|
|
|
|
|
#1
|
|
|
|
|
|
2.1.2.5. (10 pts) Compare
the values between algorithms #2 and #1, and explain why algorithm #2 consistently takes less time than
algorithm #1, given different values
of N.
2.1.2.6. (10 pts) Explain
why algorithm #3 is the
fastest among
the four.
Go to the Index
Total points= 100
1. Modify
the main( ) method in MaxSumTest.java such that the screen
output generated by the revised program resembles Table 1 above. Hints: You
may use a two-dimensional array to store the results, and then have the
values in the array displayed. Alternatively four separate one-dimensional
arrays may be used.
Note about
documentation: Proper documentation should be practiced when
writing/revising your source programs. Give appropriate information as comments
and use proper indentations. Always have your name appear at
the beginning of the program as the author or reviser of the program. Read ‘proper indentation’ in the Examples and Related
Topics page.
Note
about typesetting your documents: As
stated in the syllabus, everything you submit as part of your labs must be
typeset, including diagrams and formulas, which can be easily done using
Microsoft Word or specialized tools such as MS Visio.
1.1. (30 pts) Draw a UML class diagram to show the design
of your revised program. Clearly show the attributes
and the methods for each of the classes
in your program. Also show the associations
between the classes, if applicable. If you need a review of UML diagrams,
study the various tutorials in http://sce.uhcl.edu/yang/teaching/UML_Resources.html.
1.2. (20 pts) Draw a UML activity diagram to show the
operations involved in displaying the gathered data according to the format
as shown in Table 1. Note: Activity diagrams are
discussed in various UML tutorials. For a refresher, visit http://ias.uni-klu.ac.at/projects/uml/ECOOP99/sld121.htm
(slides 121-127).
1.3. (30 pts) Attach the revised program and
the captured screen output.
1.4. (20 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
Go to the Index
Total points= 100
1.
Chapter-end exercises: In
addition to the answers, give intermediate steps and justifications for your
answers.
1.1. (10 pts) Exercise 5.16
1.2. (10 pts) Exercise 5.19
1.3. (10 pts) Exercise 5.21
1.4. (10 pts) Exercise 5.22
1.5. (10 pts) Exercise 5.27
2. This exercise is based on the ListNode2.java program, available from http://sce.uhcl.edu/yang/teaching/JavaProgrammingExamplesandRelatedTopics.htm#linkedlist.
Complete the addSorted ( ) method, which takes a
new string and adds it into the linked list while maintaining ascending order
of the items in the list.
Use the main( ) method as shown in Figure 3.1 to test the addSorted(
) method. Sample output of running the program is shown in Figure 3.2.
public static void
main(String args[]) {
ListNode2 list = new ListNode2();
System.out.println("Creating a linked list using the addSorted( )
method ...");
list = list.addSorted("Adam");
list = list.addSorted("Eve");
list =
list.addSorted("April");
list = list.addSorted("Don");
list = list.addSorted("Syd");
list = list.addSorted("Mary");
list = list.addSorted("Peter");
list = list.addSorted("April");
list.displayAllNodes();
findAndRemove (list, "April");
System.out.println("After removing \"April\"
...");
list.displayAllNodes();
} //main
Figure 3.1:
The main( ) method for testing addSorted( )
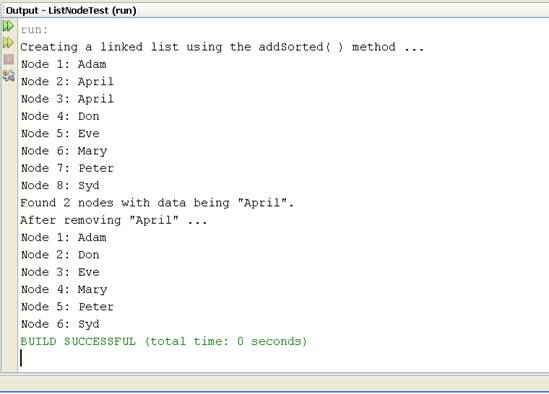
Figure 3.2:
Sample NetBeans screen output
2.1. (30 pts) Attach the revised program and
the captured screen output.
1.5. (20 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
Go to the Index
Total points= 100 + Bonus
points
1.
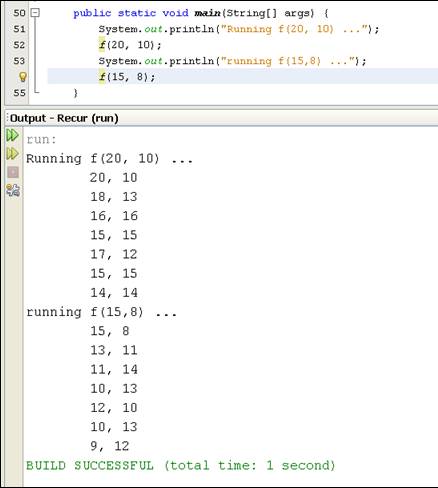
This exercise is based on the recursive function f as shown in Figure 4.1. As
discussed in class, function f can be easily implemented as a recursive
method in Java. Figure 4.2 is a sample screen output of testing a recursive
implementation of f.
|
Function f
(int m, int n)
{
Print (m, n); if
(m <= n) return 1; else
return f(m-2, n+3) + f(m-3, n+2); } |
Figure
4.1 A recursive function f
Figure 4.2 Sample output of running f( ).
1.1. (10 pts) Implement
function f( ) as a recursive function. Use the main( ) method shown in Figure 4.2 as the driver program
to test the function. Attach
the source
program and the captured screen output.
1.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
2.
The output generated by the f( ) function, as shown in Figure
4.2, does not show the respective level where each f( ) is called. Revise your f(
) function so the output will show the nested levels. In addition to printing
the values of m and
n, show the respective level. Use tab to indent the output corresponding to
the level. Figure 4.3 is a sample output of such a revised function f.
Figure 4.3 Sample output of the revised f( ), with indentation and level numbers
2.1. (10 pts) Attach
the revised program and the captured screen output.
2.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
3.
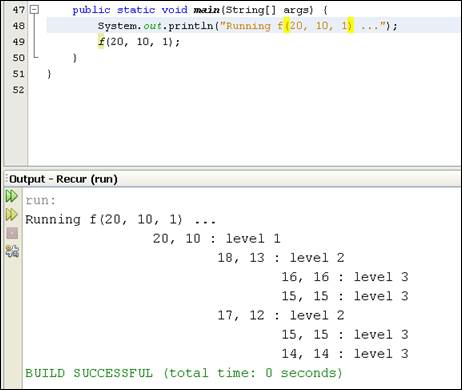
Figure 4.4 is another sample output of running the f( ) function, with parameters 20
(m), 3 (n) and 1 (initial level). The initial call of f(20,
3, 1) will trigger five levels of f( ) functions to be called.
Figure 4.4 Partial output of running f
(20, 3, 1)
3.1. (10 pts) Suppose the initial call to f( ) is considered as level 1. Given m and n, how many levels of f( ) would be invoked? For example, for the initial call f(20, 10, 1), level is 3. For the call f(20,3,1),
level is 5. Come up
with a formula to calculate the value of level, given m and n. Show how your formula is derived.
3.2. (5
pts) What is the
total number of calls to f( ), given an initial call
f (m, n, 1)?
For example, the total number of calls to f( ) as
shown in Figure 4.3 is 7 (= 1+2+4) and the number of calls in Figure 4.4 is
31 (= 1+2+4+8+16). Come up with a formula to calculate the total number of calls to f( ) given m and n. Show how your formula is
derived.
3.3. (5 pts) Suppose the dominant cost of
running function f( ) is the total number of
recursive calls. Based on your answer to 3.2 above, use the big-O notation to
show the cost of f( ). Justify your answer.
4.
A common problem with recursive functions or methods is its high cost. If not implemented right, a
recursive function can consume lots of resources, including processor time
and memory space. The primary cause of this extra overhead is
because the same function may get called more than once, triggering the same
chain of recursive calls. For example, as shown in Figure 4.4, the call
f(15,8,3) gets invoked twice; the first time by f(18,6,2) and the second time
by f(17,5,2).
4.1. (10 pts) The
getTimingInfo( ) method in the MaxSumTest.java application (Chapter 5)
is used to measure the elapsed time of running an algorithm by invoking the
algorithm multiple times and then calculating the average cost. Integrate the
getTimingInfo( ) method into your program from 2
above, such that the elapsed time of running the f( ) function can be
measured by the getTimingInfo( ) method.
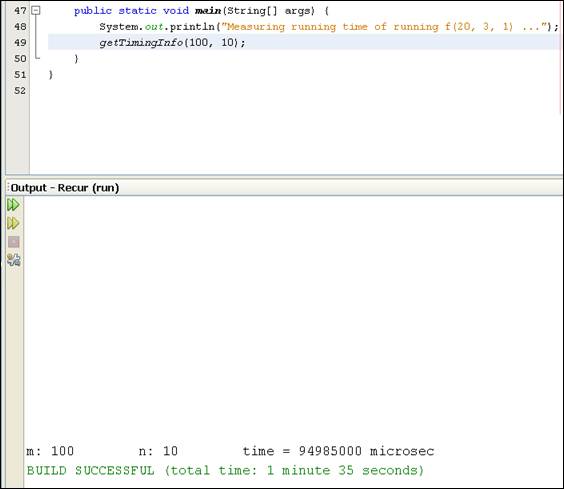
Figure 4.5 shows a sample output of running the revised program. Before the getTimingInfo( ) method returns, it prints out the
values of m and n, plus the elapsed time (in microseconds). Note: As shown in
Figure 4.5, if you run the application using NetBeans, the NetBeans system
also shows the time in minutes and seconds. Attach the revised
program and the captured screen output
of running the f( ) function, with m = 100 and n =
10.
Figure 4.5 Measuring the elapsed time of running f(100, 10, 1).
4.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
5.
To avoid
invoking the same chain of recursive function calls more than once (as
discussed in 4 above), a technique called memoization
(note: not memorization) may be used when defining a recursive function.
An array or a table may be used in implementing memoization. A[i] is used to record the returned value of f(i). When f(k) is called, the
array is examined first and, if A[k] is not set yet, A[k] is used as the
returned value of f(k); otherwise, the recursive call(s) is/are made and the
returned value is recorded in A[k].
For an introduction to memoization,
see http://xlinux.nist.gov/dads/HTML/memoize.html. In particular, read carefully how the Fibonacci
function may be implemented with memoization.
5.1. (20 pts) Use a two-dimensional array A[
][ ] to save the returned value of f( ). That is, the returned value of f(m,n,L) is saved in A[m][n]. Before making recursive
calls, if there exists a saved value in A[m][n],
that value should be used as the returned value. Attach
the revised program and the captured screen output of running the f( )
function, with m = 100 and n = 10.
5.2. (10 15 pts)
Give the TA a demo during his office hours. Be sure to give the demo before
the due date.
6.
(Bonus exercise, 10 pts) Compare
the elapsed time incurred respectively by your programs in 4 and 5 above.
What is the percentage of saving in terms of time cost?
7.
(Bonus exercise) In
principle, a recursive function can be implemented as an iterative function.
In class, both the recursive version and the iterative version of the
Fibonacci function were discussed. Derive an iterative version of the f( ) function.
7.1. (30 pts) Attach the source
program and the captured screen output
of running f(100,10,1).
7.2. (10 pts) Give the TA a demo during his office hours. Be
sure to give the demo before the due date.
7.3. (10 pts) Compare the elapsed time incurred by the iterative version of f( ) with the recursive
and the memoized recursive
versions. Which of the three is the most effective for running f(100,10,1)? Which is the slowest?
Hint: To print the hierarchical
levels as shown in Figure 4.3 and Figure 4.4, some data structure must be
used to store the intermediate values of m and n for each of the levels. The
data structure may be an array of arrays or an array of linked lists.
Method 1: Use an array of arrays to store the
intermediate values of m and n through the iteration
The array index kind of represents the level. Each
array element itself is another array to save the values of m and n for each
level.
Ø Sample call: f(20,10,1)
|
Level |
First pair of (m,n) |
2nd pair of (m,n) |
3rd pair of (m,n) |
… |
… |
|
1 |
(20, 10) |
|
|
|
|
|
2 |
(18, 13) |
(17, 12) |
|
|
|
|
3 |
(16, 16) |
(15, 15) |
(15, 15) |
(14, 14) |
|
|
4 |
|
|
|
|
|
Method 2: Use an array of linked lists to store the
intermediate values of m and n through the iteration
As shown in the figure below, the array index kind of
represents the level; while the ref points to a linked list of nodes for that
level. For example, at level one, the linked list contains only one node,
with m = 20 and n = 10; while at level two, the list contains two nodes for
the values (18,13) and (17,12).
Ø Sample call: f(20,10,1)
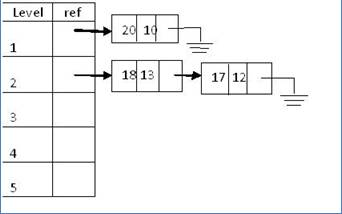
A loop is needed to “populate” this array
of lists.
Once that’s done, have another loop to print the
appropriate level and the values of m and n in the linked list.
Go to the Index
Total points= 100
1.
(5% each X 4 = 20%) Use mathematical
induction to prove the following identities of the Fibonacci sequence
(chapter 7).
1.1.
7.9a
1.2.
7.9b
1.3.
7.9d
1.4.
7.9g
2.
(5% each X 6 = 30%) Solve the
following sequences (chapter 7).
2.1.
7.17a
2.2.
7.17c
2.3.
7.18a
2.4.
7.18c
2.5.
7.19c
2.6.
7.19e
3.
(Based
on Lab 3, project 2) A linked list is a
recursively defined data structure. Each
node itself is the beginning of a linked list. For
instance, given a linked list called list,
if list.next is not null, list.next represents the beginning of
a linked list. This is true for each of the nodes in the rest of the linked
list.
As an illustration of converting an iterative method to a recursive
method, see Figure 5.1, where the
iterative version of displayAllNodes( ) is converted to displayAllNodesRecur(
int ).
public void displayAllNodesRecur (int nodeNumber)
{
ListNode2 tempNode = this;
/*
for (int i = 1; tempNode != null; tempNode = tempNode.next, i++)
{
System.out.println("Node " + i + ": " + tempNode.data);
}
//System.out.println("Leaving displayAllNodes\n");
*/
System.out.println("Node " + nodeNumber
+ ": " + tempNode.data);
if
(tempNode.next != null)
tempNode.next.displayAllNodesRecur(nodeNumber+1);
}
Figure 5.1 A recursive method to display all nodes in a linked
list
Write
a recursive method addSortedRecursive( ). Instead of using a loop to
determine where to add the new node, this method adds the new value into the
list by recursively calling itself. Figure 5.1 5.2 shows a sketch of the method.
public ListNode2 addSortedRecursive
(ListNode2 list, int value ) {
if the current node’s value is > value
create a new node and add value into it;
add
the new node in front of the current node;
return the new
node;
else
return
addSortedRecursive ( list.next, value ); //add the value to the linked
list after the current node
}
Figure 5.1 5.2 A sketch of the addSortedRecursive( ) method
Examples:
Case 1 – The list is null. In this
case, just add the new data into the list as a new node.
Case 2 – The list is not null. As an
example, suppose the list has got three nodes with data 2, 5 and 7, and we are
trying to add a new number 6 into the list. In this case, the call is addSortedRecursive(list, 6). Because the value of the first
node (2) is not > 6, a recursive call addSortedRecursive(list.next, 6) is made. In that call,
the value of the first node (5) is not > 6; therefore another recursive
call addSortedRecursive(list.next, 6) is made. In this case, the value of the first node
(7) is > 6, a new node is created with the value 6, and the new node is
inserted before the node with value 7.
Note 1: The sketch is not complete. For
example, you’ll
need to revise it so the returned linked list is correct.
Note 2: Use the main( ) method
shown in Figure 3.1 to test your
new method; replace all the calls of addSorted(
) to addSortedRecursive( ).
4.
(30 pts)
Attach the revised source program and screen output.
5.
(20 pts)
Give the TA a demo of your revised
application.
Go to the Index
Total points=100 + bonus points
1.
Chapter-end
exercises
1.1.
(10 pts)
18.2
1.2.
(10 pts)
Show the stack operations when an inorder traversal is applied to the tree
shown in Figure 18.25.
1.3.
(10 pts)
Show the stack operations when a preorder traversal is applied to the tree
shown in Figure 18.25.
1.4.
(5 pts) 18.5
1.5.
(10 pts) 8.21a.
Show your algorithm as pseudocodes.
1.6.
(10 pts)
8.21b. Show your algorithm as pseudocodes.
2.
This
exercise is based on the binary tree application from Chapter 18 of the
textbook. See http://users.cis.fiu.edu/~weiss/dsj4/code/
to find the source codes. You may also visit http://sce.uhcl.edu/yang/teaching/BinaryTreeDemo/BinaryTreeDemo.htm
to get the codes.
2.1.
Revise the
program BinaryTree.java by adding
three new methods that enables the duplication of a tree to another. Use the driver
program shown in Figure 6.1 to test your revised program. Sample output from
running the revised program is shown in Figure 6.2.
Note:
DO NOT change the driver method.
The three calls should remain the way they are. Part of your job is to create
three new methods with the proper method definitions to handle the three
calls as shown in Figure 6.1.
Hint:
Refer to the duplicate( ) method in the BinaryNode.java program. In the duplicate methods you define for the
BinaryTree class, consider calling the duplicate( ) method
defined in the BinaryNode class.
|
static public void
main(String[] args) {
BinaryTree<Integer> t1 = new BinaryTree<Integer>(1);
BinaryTree<Integer> t3 = new BinaryTree<Integer>(3);
BinaryTree<Integer> t5 = new BinaryTree<Integer>(5);
BinaryTree<Integer> t7 = new BinaryTree<Integer>(7);
BinaryTree<Integer> t2 = new BinaryTree<Integer>();
BinaryTree<Integer> t4 = new BinaryTree<Integer>();
BinaryTree<Integer> t6 = new BinaryTree<Integer>();
t2.merge(2, t1, t3);
t6.merge(6, t5, t7);
BinaryTree<Integer> t8 = new BinaryTree<Integer>(); t8 = t8.duplicateFrom(t2); //an
instance method
System.out.println("t8 from t2");
t8.printInOrder(); t8 = duplicate(t6); // a static method
System.out.println("t8 from t6");
t8.printInOrder();
t4.merge(4, t2, t6); t8 = t4.duplicate(); // an instance
method
System.out.println("t8 from t4");
t8.printInOrder();
} |
Figure 6.1 Diver method to test your revised program
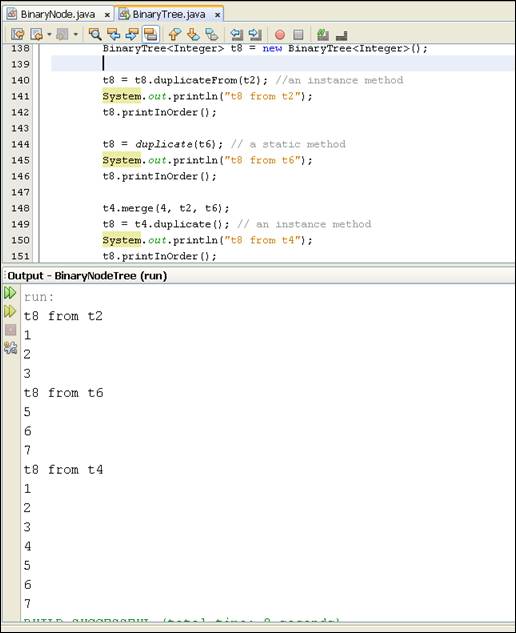
Figure
6.2 Sample output of calling the duplicate
methods
2.2.
(25 pts)
Attach the revised source program and screen output.
2.3.
(15 pts)
Give the TA a demo of your revised
application.
2.4.
(5 pts) What
are the differences between an instance method and a static method? Explain
the differences with respect to how the method is defined and called,
respectively.
3.
(Bonus project, 50 pts) 8.21c. Attach the source program and the captured
screen output.
Give the TA a demo during his office
hours. Be sure to give the demo before the due date.
Note: Your program must be working successfully to earn
the bonus points.
Go to the Index