|
T. Andrew Yang
|
last updated: 1-15-2012 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Total points= 50 (oral presentation)
+ 50 (written report) Find a topic of your interests related to ethical
issues in computer usage, development, and operations. -
Requirements: a)
Three deliverables are required of each student. See the syllabus for
the respective due dates. §
A draft of your paper – to be posted to the class discussion
board. §
An oral presentation of your topic – to be presented to the whole
class. §
A two-page paper on the topic. b)
Your paper should cite three or more technical articles. Do not
use only web links; at least two of the cited articles must be
refereed journal or conference papers. c)
Proper citing should be practiced when writing the paper. Visit http://sce.uhcl.edu/yang/citing.htm
to learn how to properly cite others’ work. Visit http://sce.uhcl.edu/yang/research/index.htm
for sample research articles. -
Grading
criteria: 1)
40% Relevance: The chosen topic must be relevant to computer ethics. 2)
30% Technical strength: The paper should be written to demonstrate your
knowledge in the chosen topic and your technical writing ability. Coherency
is especially important. 3)
30% Cited references: See b and c above. Go to the Index Total points= 100 1. (5
pts) Visit the class discussion board (link
available in the syllabus page). Post a message with your full
name as the subject line. In your post, briefly introduce yourself (including
your full name) and one item you most desire to learn in this class.
Throughout this class, you shall regularly participate at the discussion
group to find recent announcements, reminders, and discussions.
2. Algorithm Analysis
Read Chapter 5 of
the textbook. Study and understand Figure
5.3, which shows various functions in order of increasing growth rates. Assumptions: The following questions are based on a
one-dimensional array A of 155,000 integers. 2.1.1.As stated in Sec 5.6.1
in the text, the sequential search algorithm
steps through the array sequentially until a match is found or when all the
items in the array have been examined. In the latter case, the algorithm
returns ‘not found’ as the search result. Suppose you use sequential search to determine the
location of a given item n in the array (or to report that n does not exist
in the array).
2.1.1.1. (5 pts) What is
the fewest number of array items in A
that need to be examined in order to solve the problem (i.e., the best
scenario)? Justify your answer.
(That is, explain why your answer is correct.)
2.1.1.2. (5 pts) What is
the largest number of array items that need to be examined in order to solve
the problem (the worst scenario)?
Justify your answer.
2.1.1.3. (5 pts) What is
the average number of array items that need to be examined in order to solve
the problem (the average scenario)?
Justify your answer.
2.1.1.4. (10 pts) Explain
what it means by saying that the growth rate of the sequential search
algorithm is O(N). N represents the number of items in the array.
2.1.2.
Sample programs from the book are
available on line at http://users.cis.fiu.edu/~weiss/dsj4/code/.
The following set of exercises are based on the program MaxSumTest.java, which is one of the sample applications for
Chapter 5. Visit http://users.cis.fiu.edu/~weiss/dsj4/code/MaxSumTest.java
to download it directly (local
copy).
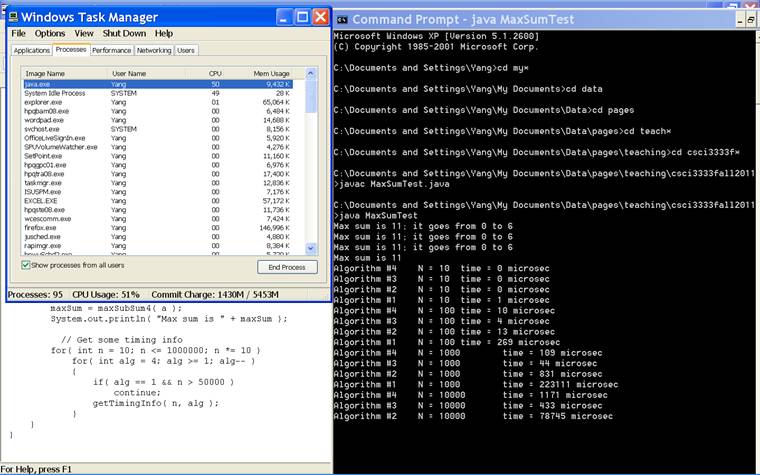
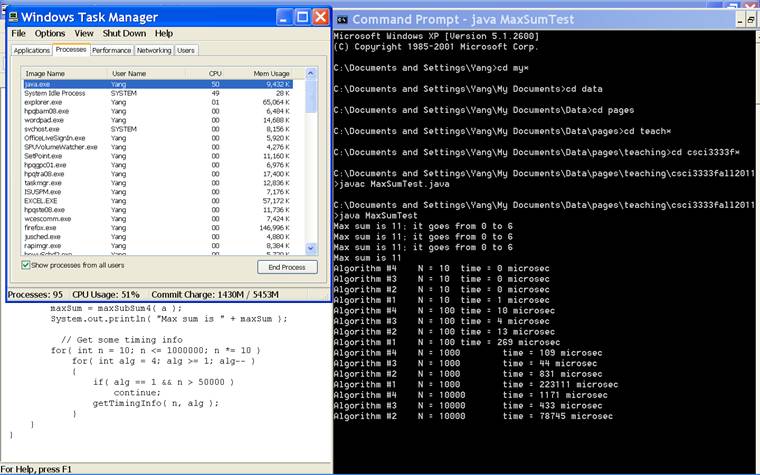
2.1.2.1. (10 pts) Run MaxSumTest.java and capture the screen snapshot
showing the complete execution of that application. Attach the
captured snapshot.
Note: The captured screen snapshot should show that the java program is
using a high percentage of the computer’s CPU. You may use Windows Task
Manager to see that. A sample snapshot showing partial execution of
the program and the cpu usage by that program is shown below.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Size of N
Algorithms
|
250
|
2500
|
25000
|
250000
|
#4
|
|
|
|
|
#3
|
|
|
|
|
#2
|
|
|
|
|
#1
|
|
|
|
|
2.1.2.5. (10 pts) Compare
the values between algorithms #2 and #1, and explain why algorithm #2 consistently takes less time than
algorithm #1, given different values
of N.
2.1.2.6. (10 pts) Explain
why algorithm #3 is the
fastest among
the four.
Go to the Index
Total points= 100
1. Modify
the main( ) method in MaxSumTest.java such that the screen
output generated by the revised program resembles Table 1 above. Hints: You
may use a two-dimensional array to store the results, and then have the values
in the array displayed. Alternatively four separate one-dimensional arrays
may be used.
Note about
documentation: Proper documentation should be practiced when
writing/revising your source programs. Give appropriate information as comments
and use proper indentations. Always have your name appear at
the beginning of the program as the author or reviser of the program. Read ‘proper indentation’ in the Examples and Related
Topics page.
Note
about typesetting your documents: As
stated in the syllabus, everything you submit as part of your labs must be typeset, including diagrams and formulas,
which can be easily done using Microsoft Word or specialized tools such as MS
Visio.
1.1. (30 pts) Draw a UML class diagram to show the design
of your revised program. Clearly show the attributes
and the methods for each of the
classes in your program. Also show the associations
between the classes, if applicable. If you need a review of UML diagrams,
study the various tutorials in http://sce.uhcl.edu/yang/teaching/UML_Resources.html.
1.2. (20 pts) Draw a UML activity diagram to show the
operations involved in displaying the gathered data according to the format
as shown in Table 1. Note: Activity diagrams are
discussed in various UML tutorials. For a refresher, visit http://ias.uni-klu.ac.at/projects/uml/ECOOP99/sld121.htm
(slides 121-127).
1.3. (30 pts) Attach the revised program and
the captured screen output.
1.4. (20 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
Go to the Index
Total points= 100
1. This exercise is based on the ListNode2.java program, available from http://sce.uhcl.edu/yang/teaching/JavaProgrammingExamplesandRelatedTopics.htm#linkedlist.
Complete the addSorted ( ) method, which takes a
new string and adds it into the linked list while maintaining ascending order
of the items in the list.
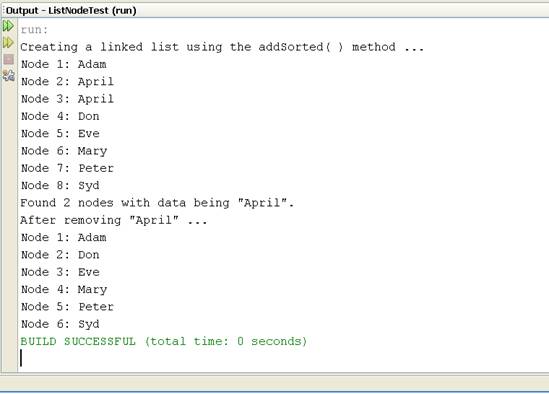
Use the main( )
method as shown in Figure 3.1 to
test the addSorted( ) method.
Sample output of running the program is shown in Figure 3.2.
public static void
main(String args[]) {
ListNode2 list = new ListNode2();
System.out.println("Creating a linked list using the addSorted( )
method ...");
list = list.addSorted("Adam");
list = list.addSorted("Eve");
list = list.addSorted("April");
list = list.addSorted("Don");
list = list.addSorted("Syd");
list = list.addSorted("Mary");
list = list.addSorted("Peter");
list = list.addSorted("April");
list.displayAllNodes();
findAndRemove (list, "April");
System.out.println("After removing \"April\"
...");
list.displayAllNodes();
} //main
Figure 3.1:
The main( ) method for testing addSorted( )
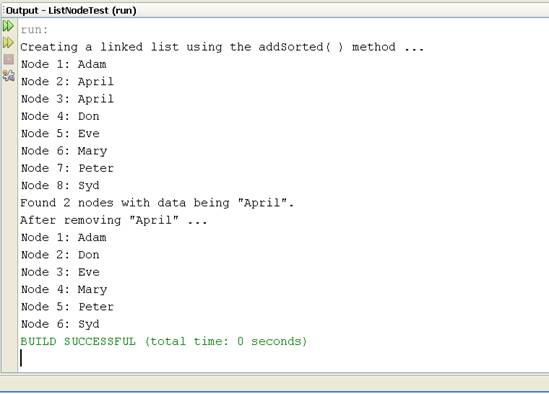
Figure 3.2:
Sample NetBeans screen output
1.1. (30 pts) Attach the revised program and
the captured screen output.
1.2. (20 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
2.
Chapter-end exercises: In
addition to the answers, give intermediate steps and justifications for your
answers.
2.1. (10 pts) For 2,500
items, an algorithm takes 10 seconds to run on machine A, but now you replace
the machine with machine B that is 3 times as fast. Approximately how long
will the algorithm take to run on machine B for 6,000 items if the algorithm
is linear?
2.2. (10 pts) For 2,500
items, an algorithm takes 10 seconds to run on machine A, but now you replace
the machine with machine B that is 3 times as fast. Approximately how long
will the algorithm take to run on machine B for 6,000 items if the algorithm
is quadratic?
2.3. (10 pts) Exercise 5.19
2.4. (10 pts) Exercise 5.21
2.5. (10 pts) Exercise 5.27
3.
(Bonus,
10 pts) For 2,000 items, an algorithm takes 10
seconds to run on machine A, but now you replace the machine with machine B
that is 3 times as fast. Approximately how long will the algorithm take to
run on machine B for 6,000 items if the algorithm is O(N (log N)2 )?
Go to the Index
Total points= 100 + Bonus
points
1.
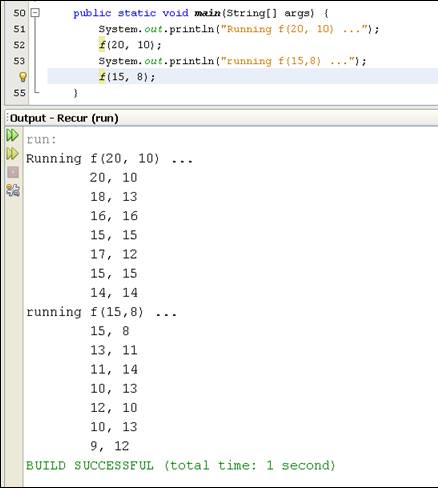
This exercise is based on the recursive function f as shown in Figure 4.1. As
discussed in class, function f can be easily implemented as a recursive
method in Java. Figure 4.2 is a sample screen output of testing a recursive
implementation of f.
|
Function f
(int m, int n)
{
Print (m, n); if
(m <= n) return 1; else
return f(m-2, n+3) + f(m-3, n+2); } |
Figure
4.1 A recursive function f
Figure 4.2 Sample output of running f( ).
1.1. (10 pts) Implement
function f( ) as a
recursive function. Use the main( ) method shown in Figure 4.2 as the driver
program to test the function. Attach
the source
program and the captured screen output.
1.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
2.
The output generated by the f( ) function, as shown in Figure
4.2, does not show the respective level where each f( ) is called. Revise your f( ) function so
the output will show the nested levels. In addition to printing
the values of m and
n, show the respective level. Use tab to indent the output corresponding to
the level. Figure 4.3 is a sample output of such a revised function f.
Figure 4.3 Sample output of the revised f( ),
with indentation and level numbers
2.1. (10 pts) Attach
the revised program and the captured screen output.
2.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
3.
Figure 4.4 is another sample output of running the f(
) function, with
parameters 20 (m), 3 (n) and 1 (initial level).
The initial call of f(20, 3, 1) will trigger five levels of f( ) functions to
be called.
Figure 4.4 Partial output of running f
(20, 3, 1)
3.1. (10 pts) Suppose the initial call to f( )
is considered as level 1. Given m and
n, how many levels of
f( ) would be
invoked? For
example, for the initial call f(20, 10, 1), level is 3. For the call f(20,3,1),
level is 5. Come up
with a formula to calculate the value of level, given m and n. Show how your formula is derived.
3.2. (5
pts) What is the
total number of calls to f( ), given an initial call f (m, n, 1)? For example, the total number
of calls to f( ) as shown in Figure 4.3 is 7 (= 1+2+4) and the number of
calls in Figure 4.4 is 31 (= 1+2+4+8+16). Come up with a formula to calculate
the total number of calls to f( )
given m and n. Show how your formula is derived.
3.3. (5 pts) Suppose the dominant cost of
running function f( ) is the total number of recursive calls. Based on your
answer to 3.2 above, use the big-O notation to show the cost of f( ). Justify
your answer.
4.
A common problem with recursive functions or methods is its high cost. If not implemented right, a
recursive function can consume lots of resources, including processor time
and memory space. The primary cause of this extra overhead is
because the same function may get called more than once, triggering the same
chain of recursive calls. For example, as shown in Figure 4.4, the call
f(15,8,3) gets invoked twice; the first time by f(18,6,2) and the second time
by f(17,5,2).
4.1. (10 pts) The
getTimingInfo( ) method in the MaxSumTest.java application (Chapter 5)
is used to measure the elapsed time of running an algorithm by invoking the
algorithm multiple times and then calculating the average cost. Integrate the
getTimingInfo( ) method into your program from 2 above, such that the elapsed
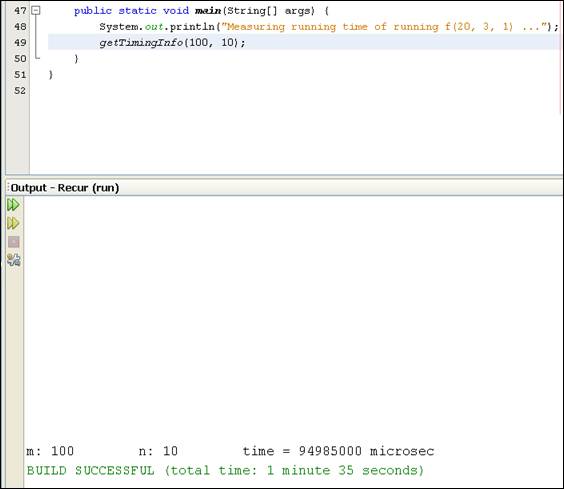
time of running the f( ) function can be measured by the getTimingInfo( ) method. Figure 4.5 shows a sample output of
running the revised program. Before the getTimingInfo(
) method returns, it prints out the values of m and n, plus the elapsed
time (in microseconds). Note: As shown in Figure 4.5, if you run the
application using NetBeans, the NetBeans system also shows the time in
minutes and seconds. Attach the revised program and the captured screen
output of running the f( ) function,
with m = 100 and n = 10.
Figure 4.5 Measuring the elapsed time of
running f(100, 10, 1).
4.2. (5 pts) Give the TA a demo during his
office hours. Be sure to give the demo before the due date.
5.
To avoid
invoking the same chain of recursive function calls more than once (as
discussed in 4 above), a technique called memoization
(note: not memorization) may be used when defining a recursive function.
An array or a table may be used in implementing memoization. A[i] is used to record the returned value of f(i).
When f(k) is called, the array is examined first and, if A[k] is not set yet,
A[k] is used as the returned value of f(k); otherwise, the recursive call(s)
is/are made and the returned value is recorded in A[k].
For an introduction to memoization,
see http://xlinux.nist.gov/dads/HTML/memoize.html. In particular, read carefully how the Fibonacci
function may be implemented with memoization.
5.1. (20 pts) Use a two-dimensional array A[ ][ ] to save the
returned value of f( ). That is, the returned value of f(m,n,L) is saved in
A[m][n]. Before making recursive calls, if there exists a saved value in
A[m][n], that value should be used as the returned value. Attach
the revised program and the captured screen output of running the f( ) function, with m = 100 and n
= 10.
5.2. (15 pts) Give
the TA a demo during his office hours. Be sure to give the demo before the
due date.
6.
(Bonus exercise, 10 pts) Compare
the elapsed time incurred respectively by your programs in 4 and 5 above.
What is the percentage of saving in terms of time cost?
7.
(Bonus exercise) In
principle, a recursive function can be implemented as an iterative function.
In class, both the recursive version and the iterative version of the
Fibonacci function were discussed. Derive an iterative version of the f( )
function.
7.1. (30 pts) Attach the source
program and the captured screen output
of running f(100,10,1).
7.2. (10 pts) Give the TA a demo during his office hours. Be
sure to give the demo before the due date.
7.3. (10 pts) Compare the elapsed time incurred by the iterative version of f( ) with the recursive and the memoized recursive versions. Which of the three is the most
effective for running f(100,10,1)? Which is the slowest?
Hint: To print the hierarchical
levels as shown in Figure 4.3 and Figure 4.4, some data structure must be
used to store the intermediate values of m
and n for each of the levels. The
data structure may be an array of arrays or an array of linked lists.
Method 1: Use an array of arrays to store the
intermediate values of m and n through the iterations.
The array index kind of represents the level. Each array
element itself is another array to save the values of m and n for each level.
Ø Sample call: f(20,10,1)
|
Level |
First pair of (m,n) |
2nd pair of (m,n) |
3rd pair of (m,n) |
… |
… |
|
1 |
(20, 10) |
|
|
|
|
|
2 |
(18, 13) |
(17, 12) |
|
|
|
|
3 |
(16, 16) |
(15, 15) |
(15, 15) |
(14, 14) |
|
|
4 |
|
|
|
|
|
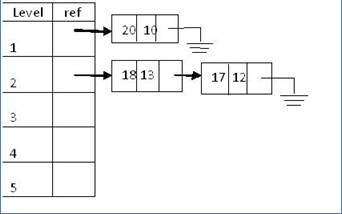
Method 2: Use an array of linked lists to store the
intermediate values of m and n through the iterations.
As shown in the figure below, the array index kind of represents
the level; while the ref points to a linked list of nodes for that level. For
example, at level one, the linked list contains only one node, with m = 20
and n = 10; while at level two, the list contains two nodes for the values
(18,13) and (17,12).
Ø Sample call: f(20,10,1)
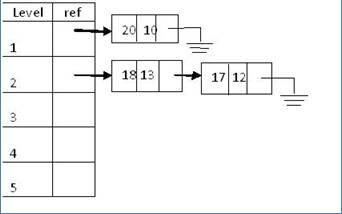
A loop is needed to “populate” this array
of lists.
Once that’s done, have another loop to print the
appropriate level and the values of m and n in the linked list.
Go to the Index
Total points= 100
1.
(Based on Lab 3, project 2) A linked list is a recursively defined data
structure. Each node itself is the
beginning of a linked list. For
instance, given a linked list called list,
if list.next is not null, list.next represents the beginning of
a linked list. This is true for each of the nodes in the rest of the linked
list.
As an illustration of converting an
iterative method to a recursive method, see Figure 5.1, where the iterative version of displayAllNodes( ) is
converted to displayAllNodesRecur( int ).
public void displayAllNodesRecur
(int nodeNumber) {
ListNode2 tempNode = this;
/*
for (int i = 1; tempNode != null; tempNode = tempNode.next, i++) {
System.out.println("Node " + i + ": " +
tempNode.data);
}
//System.out.println("Leaving
displayAllNodes\n");
*/
System.out.println("Node " + nodeNumber + ": " +
tempNode.data);
if
(tempNode.next != null)
tempNode.next.displayAllNodesRecur(nodeNumber+1);
}
Figure 5.1 A recursive method to display
all nodes in a linked list
Write
a recursive method addSortedRecursive(
). Instead of using a loop to determine where to add the new node, this
method adds the new value into the list by recursively calling itself.
Figure 5.2 shows a sketch
of the method.
public ListNode2 addSortedRecursive
(ListNode2 list, int value ) {
if the current node’s value is > value
create a new node and add value into it;
add
the new node in front of the current node;
return the new
node;
else
return
addSortedRecursive ( list.next, value ); //add the value to the linked
list after the current node
}
Figure 5.2
A sketch of the addSortedRecursive( ) method
Examples:
Case 1 – The
list is null. In this case, just add the new data into the list as a new
node.
Case 2 – The
list is not null. As an example, suppose the list has got three nodes with
data 2, 5 and 7, and we are trying to add a new number 6 into the list. In
this case, the call is addSortedRecursive(list, 6). Because the value of the
first node (2) is not > 6, a recursive call addSortedRecursive(list.next, 6) is made. In that call,
the value of the first node (5) is not > 6; therefore another recursive
call addSortedRecursive(list.next,
6) is made. In this case, the value of the first node (7) is > 6, a new
node is created with the value 6, and the new node is inserted before the
node with value 7.
Note
1: The
sketch is not complete. For example, you’ll need to revise it so the
returned linked list is correct.
Note 2: Use the main( ) method shown in Figure 3.1 to test your new method;
replace all the calls of addSorted( )
to addSortedRecursive( ).
1.1.
(30 pts)
Attach the revised source program and screen output.
1.2.
(20 pts)
Give the TA a demo of your revised
application.
2.
Use
mathematical induction to prove the following identities of the Fibonacci
sequence (chapter 7).
2.1.
(5%) 7.9a
2.2.
(5%) 7.9g
3.
Solve the
following sequences (chapter 7).
3.1.
(5%) 7.17a
3.2.
(5%) 7.18c
3.3.
(5%) 7.19d
4.
The
following questions are based on the tree in Figure 18.33 (page 682):
4.1.
(1%) List
the siblings of node J.
4.2.
(1%) List
the children of node J.
4.3.
(1%) What
is the height of node J?
4.4.
(1%) What
is the depth of node J?
4.5.
(1%) What
is the size of node J?
5.
(10 pts) 18.5
6.
(10 pts) 18.6
Go to the Index
Total points=100 + bonus points
1.
This exercise
is based on the binary tree application from Chapter 18 of the textbook. See http://users.cis.fiu.edu/~weiss/dsj4/code/
to find the source codes. You may also visit http://sce.uhcl.edu/yang/teaching/BinaryTreeDemo/BinaryTreeDemo.htm
to get the codes.
1.1.
Revise the
program BinaryTree.java by adding three
new methods that enables the duplication of a tree to another. Use the driver
program shown in Figure 6.1 to test your revised program. Sample output from
running the revised program is shown in Figure 6.2.
Note:
DO NOT change the driver method. The
three calls should remain the way they are. Part of your job is to create
three new methods with the proper method definitions to handle the three
calls as shown in Figure 6.1.
Hint:
Refer to the duplicate( ) method in the BinaryNode.java program. In the duplicate methods you define for the
BinaryTree class, consider calling the duplicate(
) method defined in the BinaryNode class.
|
static public void
main(String[] args) {
BinaryTree<Integer> t1 = new BinaryTree<Integer>(1);
BinaryTree<Integer> t3 = new BinaryTree<Integer>(3);
BinaryTree<Integer> t5 = new BinaryTree<Integer>(5);
BinaryTree<Integer> t7 = new BinaryTree<Integer>(7);
BinaryTree<Integer> t2 = new BinaryTree<Integer>();
BinaryTree<Integer> t4 = new BinaryTree<Integer>();
BinaryTree<Integer> t6 = new BinaryTree<Integer>();
t2.merge(2, t1, t3);
t6.merge(6, t5, t7);
BinaryTree<Integer> t8 = new BinaryTree<Integer>(); t8 = t8.duplicateFrom(t2); //an
instance method
System.out.println("t8 from t2");
t8.printInOrder(); t8 = duplicate(t6); // a static method
System.out.println("t8 from t6");
t8.printInOrder();
t4.merge(4, t2, t6); t8 = t4.duplicate(); // an instance
method
System.out.println("t8 from t4");
t8.printInOrder();
} |
Figure 6.1 Diver method to test your revised program
Figure
6.2 Sample output of calling the duplicate
methods
1.2.
(25 pts)
Attach the revised source program and screen output.
1.3.
(15 pts)
Give the TA a demo of your revised
application.
1.4.
(5 pts) What
are the differences between an instance method and a static method? Explain
the differences with respect to how the method is defined and called,
respectively.
2.
Chapter-end
exercises
2.1.
(10 pts)
Show the stack operations when a preorder traversal is applied to the tree
shown in Figure 18.25.
2.2.
(10 pts) The
quicksort algorithm is presented in
the textbook as Figure 8.22; an implementation of the algorithm can be found
in http://sceweb.uhcl.edu/yang/teaching/SortingDemo/SortDemo.htm,
which uses an array of 20 integers to test the algorithm. Run that
application by using an array of 30 integers. Hand in the revised program and
the generated screen output.
2.3.
(10 pts) 8.16. Justify your answer.
2.4.
(10 pts) 8.21b. Show your algorithm as pseudo
codes.
2.5.
(10 pts) 20.5b.
2.6.
(5 pts) 20.14. Justify your answer.
Go to the Index