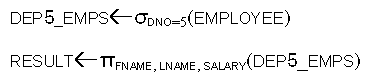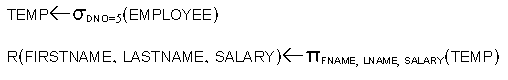7.3. The Relational Algebra

• A sequence of relational algebra operations forms a relational algebra expression, whose result will also be a relation .
  

• Set-oriented operations: UNION, INTERSECTION, and SET DIFFERENCE. 

• Operations developed specifically for relational databases: SELECT, PROJECT, and JOIN, etc.

Operations	Symbols	Sample Expressions
select
project
rename
union
intersection
difference	-
theta join
natural join	*
division

---

• The SELECT operation is used to select a subset of the tuples from a relation that satisfy a selection condition. One can consider the SELECT operation to be a filter that keeps only those tuples that satisfy a qualifying condition.
  

• The SELECT operator is unary; that is, it is applied to a single relation.
  

• The degree of the relation resulting from a SELECT operation is the same as that of R. The number of tuples in the resulting relation is always less than or equal to the number of tuples in R.
  

• The SELECT operation is commutative.
  

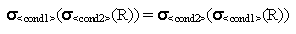
• Hence, a sequence of SELECTs can be applied in any order.  In addition, we can always combine a cascade of SELECT operations into a single SELECT operation with a conjunctive (AND) condition

---

• The PROJECT operation selects certain columns from the table and discards the other columns.
  

• If the attribute list includes only nonkey attributes of R, duplicate tuples are likely to occur; the PROJECT operation removes any duplicate tuples, so the result of the PROJECT operation is a set of tuples and hence a valid relation. This is known as duplicate elimination .
  

• 
  

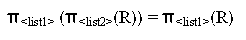
• Commutativity does not hold on PROJECT .
  

---

• Sequence of Operations versus Renaming:
  

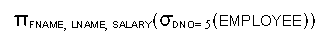
c.f.,

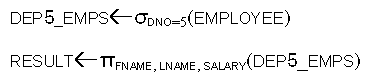
• To rename the attributes in the intermediate and result relations:
  

---

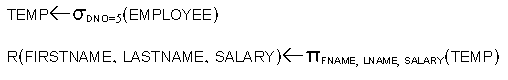
• The UNION operation combines two or more relations into a single relation.
  

Constraints?

Union compatibility : Two relations R(A1, A2, . . ., An) and S(B1, B2, . . ., Bn) are said to be union compatible if they have the same degree n, and if dom(Ai) = dom(Bi) for all i, i >=1 and i <= n.

The two relations on which any of the set-oriented operations (UNION, INTERSECTION, and SET DIFFERENCE) are applied must be union compatible.

• INTERSECTION: The result of this operation is a relation that includes all tuples that are in both R and S.
  

• SET DIFFERENCE: The result of this operation, denoted by R - S, is a relation that includes all tuples that are in R but not in S.
  

• Examples: See Fig. 7.11 (p.218)
  

• Both UNION and INTERSECTION are commutative operations, but DIFFERENCE is not.
  

• Both UNION and INTERSECTION  are associative operations.
  

---

• The CARTESIAN PRODUCT operation is also known as CROSS PRODUCT or CROSS JOIN.
  

• The CARTESIAN PRODUCT operation is used to combine tuples from two relations in a combinatorial fashion.
  

• Example:
  

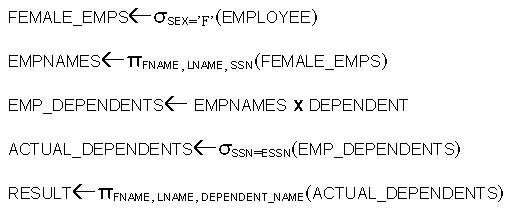
• Because this sequence of CARTESIAN PRODUCT followed by SELECT is used quite commonly to identify and select related tuples from two relations, a special operation, called JOIN, was created to specify this sequence as a single operation.
  

---

• The JOIN operation is used to combine related tuples from two relations into single tuples.
  

• Example:
  

c.f.,

• What makes a JOIN different from a CARTESIAN PRODUCT?
  

• General join condition s
  

• A JOIN operation with a general join condition is called a THETA JOIN.
  

• The most common JOIN involves join conditions with equality comparisons only. Such a JOIN, where the only comparison operator used is =, is called an EQUIJOIN .
  

• NATURAL JOIN is basically an EQUIJOIN followed by removal of the superfluous attributes.

Example:

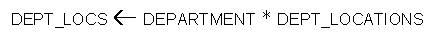
(See the result in Fig. 7.14(b), p.222)

• Exercises:
  

Write down the relational operation of the following database query, posted against the relational database state in Fig. 7.6, p.205:

• Show the full name of the employees who have worked for 20 or more hours in any projects.

• Show the names, SSNs and dependents information of all employees who were born after "1965-01-01".
  

---

• The DIVISION operation is useful for queries such as "Retrieve the names of employees who work on all the projects that ‘John Smith’ works on."
  

• Formal definition: See p.224.
  

• Example: See Fig. 7.15 (b), p.225.
  

---

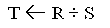
• Aggregate Functions and Grouping

• Aggregate functions, in the context of relational database model, are common functions applied to collections of numeric values, such as SUM, AVERAGE, MAXIMUM, and MINIMUM.

• The COUNT aggregate function is used for counting tuples or values. 

• Grouping is an operation that groups the tuples in a relation by the value of some of their attributes.

• A common operation is to apply grouping to a relation and then apply an aggregate function independently to each group.  An example: ( i ) Group employee tuples by DNO, so that each group includes the tuples for employees working in the same department. ( ii ) Apply the AVERAGE aggregate function to the groups to list the average salary of employees within each of the departments. 

• Formal notation: 

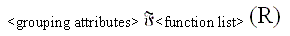
• The resulting relation has the grouping attributes plus one attribute for each element in the function list.

• Example: 

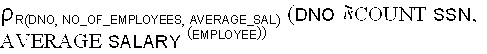
The result: A relation that contains each department number, the number of employees in the department, and their average salary .   (See Fig. 7.16a)

• Question: How would you specify a query for calculating the average salary of ALL employees?

---

• Recursive Closure Operations
  

• This operation is applied to a recursive relationship between tuples of the same type, such as the relationship between an employee and a supervisor.

• Example: To retrieve all supervisees of an employee at ALL levels .

• NOTE: In the basic relational algebra, it is impossible to specify such recursive closure operations.

• Recursive queries will be further discussed in Chapter 25 when we give an overview of deductive databases.

• The SQL3 standard includes syntax for recursive closure.
  

• Outer Join
  

• A LEFT OUTER JOIN keeps every tuple in the first (or left) relation in the result.  If no matching tuple is found in the second (or right) relation, then the attributes of the second relation in the join result are filled with null values.    (Compare: Natural Join)

• Example of a LEFT OUTER JOIN: To retrieve a list of all employee names and also the name of the departments they manage if they happen to manage a department. 

• A RIGHT OUTER JOIN keeps every tuple in the second (or right) relation in the result.  

• A FULL OUTER JOIN keeps all tuples in both the left and the right relations.  When no matching tuples are found, padding them with null values as needed. 

• The three outer join operations are part of the SQL2 standard .

---

• Outer Union

• The OUTER UNION operation was developed to take the union of tuples from two relations if the relations are not union compatible .

• For example, an OUTER UNION can be applied to two relations whose schemas are STUDENT(Name, SSN, Department, Advisor) and FACULTY(Name, SSN, Department, Rank). 

• The resulting relation schema is R(Name, SSN, Department, Advisor, Rank), and all the tuples from both relations are included in the result. Student tuples will have a null for the Rank attribute, whereas faculty tuples will have a null for the Advisor attribute.
  

See Fig. 7.18:

---

Ø Go to the Index