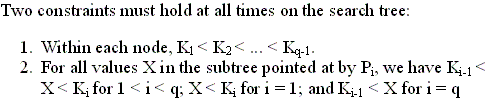CSCI 5333 Data Base Management System
Spring 2002 (1/14-5/6)
Chapter 6: Index Structures
14.1 Types of Single-Level Ordered
Indexes
- Compare: primary index, clustering index, secondary
index (See Table 14.1, and Table 14.2)
14.2 Multilevel Indexes
- Example: Indexed sequential file, ISAM (See Fig.
14.6)
- Exercise: Examine Figure 14.6. If the search
key is 36, how many disk retrieval operations are needed to
find the block? How if the search key is inexistent
in the file?
- Question: Review question 14.4.
14.3 Dynamic Multilevel Indexes Using B-Trees and B+-Trees
- 14.3.1 Search Trees and B-Trees
- Search Trees: See Figure 14.8, and Figure 14.9.
- Question: How is a search tree used as a mechanism
for searching for a record in a file or disk blocks containing
the record?
- Balanced search tree: All of its leaf nodes are
at the same level.
- Problems with search trees:
- The inserting and deleting algorithms do not guarantee
the search tree is balanced.
- Record deletion may leave some nodes in the tree
nearly empty, thus wasting storage space and increasing the number of
levels.
- Question: What's wrong with increased number
of levels?
- With the addition of data pointers, a B-tree
has additional constraints that ensure that the tree is
always balanced and that the space wasted by deletion,
if any, never becomes excessive.
- Question: What's the purpose of data pointers?
- Insertion: possible propagation of node splitting
(up) and increase of tree levels
- Deletion: possible propagation of node combining,
and reduction of tree levels
- Exercises: Example 4 and 5.
- Data pointers are stored only at the leaf nodes of the
tree; hence, the structure of leaf nodes differs from
the structure of internal nodes.
- The pointers in internal nodes are tree pointers
to blocks that are tree nodes, whereas the pointers in
leaf nodes are data pointers to the data file records
or blocks—except for the Pnext pointer, which is
a tree pointer to the next leaf node.
- Question: How is ordered access provided in B+-trees?
- Algorithm 14.2: Searching algorithm.
- Algorithm 14.3: Insertion (Also see Fig. 14.12.)
- Deletion example: Fig. 14.13
- Compare B-trees and B+-trees
14.4 Indexes on Multiple Keys
Go
to the
Index
|
Main Page
Biography
Teaching
Research
Services
Other Links
|
